JEE 2018 :: Physics (2018) :: Solved questions 2018

• Physics (2018) - Solved questions 2018

In the figure  below , the switches S₁ and S₂  are closed simultaneously  at t=0 and  a current starts to flow in the circuit.  Both the batteries have  the same magnitude of the electromotive force (emf) and the polarities are as indicated in the figure. Ignore mutual inductance between the inductors. The current I in the middle wires reaches its maximum magnitude I_max at time $t=\tau$ . which of the following statements is (are) true ?

Answer:

Explanation:

$I_{1}=\frac{V}{R}(1-e^-{\frac{tR}{L}}$

$I_{2}=\frac{V}{R}(1-e^-{\frac{tR}{2L})}$

  From principle of superposition,

$I=I_{1}-I_{2}\Rightarrow I=\frac{V}{R}e^{-\frac{tR}{2L}}(1-e^{-\frac{tR}{2L}})$        .......(i)

I is maximum when $\frac{\text{d}I}{\text{d}t}=0$ , which gives

$e^{-\frac{IR}{2L}}=\frac{1}{2}$   or  $t =\frac{2L}{R}In 2$

 Substituting this time in Eq. (i), we get

      $I_{max}=\frac{V}{4R}$

A uniform capillary tube of inner radius r is dipped vertically in to a beaker filled with water. The water rises  to a height  h in the capillary tube above the water surface in the beaker. The surface tension of the water is $\sigma$ . The angle of contact between water and the wall of the capillary tube is θ . Ignore the mass of water in the meniscus. Which of the following statements is (are)  true ?

Answer:

Explanation:

$h=\frac{2\sigma\cos\theta}{r\rho g}$

$(a)   \rightarrow  h\alpha\frac{1}{r}$

 (b) h depends upon  $\sigma$

(c)   If lift is going up with  constant acceleration

    $g_{eff}= (g+a)\Rightarrow h= \frac{2\sigma \cos\theta}{r\rho (g+a)}$

    It means h decreases.

(d)  h is proportional $\cos\theta$

The potential energy of mass m at a distance r from a fixed point O is  given  by $V(r)=\frac{kr^{2}}{2}$ , where k is a positive constant of appropriate dimensions.  This particle is moving in a circular orbit of radius R  about the point O. If v is the speed of the particle and L is the magnitude of its angular momentum about O, which of the following statements is (are) true?

Answer:

Explanation:

$V=\frac{Kr^{2}}{2}$

$F=-\frac{\text{d}V}{\text{d}r}= -Kr$   [ towars centre]

                                                 [ $F=-\frac{\text{d}V}{\text{d}r}$ ]

$kR= \frac{mv^{2}}{R}$  [Centripetal force ]

$v=\sqrt{\frac{kR^{2}}{m}}=\sqrt{\frac{k}{m}}R$

  $\Rightarrow$                      $L=mvR=\sqrt{\frac{k}{m}}R^{2}$

Two batteries with emf 12V and 13V are connected in parallel across a load resistor of 10 Ω . The internal resistances of the two batteries are 1Ω and 2Ω, respectively. The voltage across the load lies between

Answer:

Explanation:

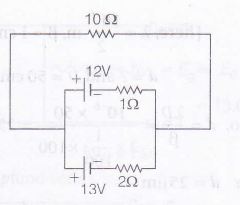
for parallel combination of cells,

$E_{eq}=\frac{\frac{E_{1}}{r_{1}}+\frac{E_{2}}{r_{2}}}{\frac{1}{r_{1}}+\frac{1}{r_{2}}}$

$\therefore$        $E_{eq}=\frac{\frac{12_{}}{1_{}}+\frac{13_{}}{2_{}}}{\frac{1}{1_{}}+\frac{1}{2_{}}}=\frac{37}{2} V$

Potential drop across 10Ω resistance,

  V= ($\frac{E}{R_{total}}$) $\times 10$

    = $\frac{\frac{37}{3}}{(10+\frac{2}{3})}\times 10=11.56 V$

$\therefore$      V= 11.56V

Alternative Method

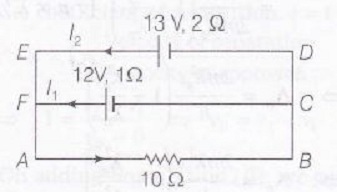
Applying KVL,

in Loop        ABCDFA,

  $-12+10(I_{1}+I_{2})+1\times I_{1}=0$

$\Rightarrow$        $12=11I_{1}-10I_{2}$     .......(i)

Similarly.

in loop ABCDEA,

$-13+10(I_{1}+I_{2})+2\times I_{2}=0$

$\Rightarrow$       $13=10I_{1}+12I_{2}$             ...........(ii)

Solving Eqs. (i) and (ii), we get

$I_{1}=\frac{7}{16}A, I_{2}=\frac{23}{32}A$

 Voltage drop across 10Ω resistance is,

$V=10[\frac{7}{16}+\frac{23}{32}]=11.56V$

On interchanging the resistances, the balance point of a meter bridge shifts to the left by 10cm. The resistance of their series combination is 1kΩ. How much was the resistance on the left slot before interchanging the resistances?

Answer:

Explanation:

We have X+Y=1000Ω

Initially,   $\frac{X}{l}=\frac{1000-X}{100-l}$         ..............(i)

 When X and Y  are interchanged, then

 $\frac{1000-X}{l-10}=\frac{X}{100-(l-10)}$

OR    $\frac{1000-X}{l-10}=\frac{X}{110-l}$        .........(ii)

 From Eqs. (i) and (ii), we get

$\frac{100-l}{l}=\frac{l-10}{110-l}$

$\left(100-l\right)\left(110-l\right)$ = $\left(l-10\right)l$

$11000-100l -110l+l^{2}=l^{2}-10l$

$\Rightarrow$        $11000=200l$

$\therefore$             $l=55 cm$

Substituting the value of l in Eq. (i), we get

$\frac{X}{55}=\frac{1000-55}{100-55}$

$\Rightarrow$          20X=11000

                                 X= 550Ω

• Physics (2018) - Solved questions 2018